หุ่นยนต์ปรับสมดุลตนเองโดยใช้อัลกอริทึม PID (STM MC): 9 ขั้นตอน

2024 ผู้เขียน: John Day | [email protected]. แก้ไขล่าสุด: 2024-01-30 13:07

เมื่อเร็ว ๆ นี้มีการทำงานมากมายในการปรับสมดุลของวัตถุ แนวคิดของการทรงตัวในตนเองเริ่มต้นจากการทรงตัวของลูกตุ้มคว่ำ แนวคิดนี้ขยายไปถึงการออกแบบเครื่องบินด้วย ในโครงการนี้ เราได้ออกแบบหุ่นยนต์สร้างสมดุลในตัวเองขนาดเล็กโดยใช้อัลกอริธึม PID(Proportional, Integral, Derivative) ตั้งแต่นั้นมา วิธีการนี้เป็นหน้าใหม่ของระบบควบคุมกระบวนการทางอุตสาหกรรม รายงานนี้ทบทวนวิธีการที่เกี่ยวข้องกับการปรับสมดุลของวัตถุ โครงการนี้จัดทำขึ้นเป็นโครงการภาคการศึกษาเพื่อทำความเข้าใจความสัมพันธ์ของ PID ต่อประสิทธิภาพของกระบวนการทางอุตสาหกรรมต่างๆ ในที่นี้ เราเน้นเฉพาะการทบทวนสั้นๆ เกี่ยวกับประสิทธิภาพและการประยุกต์ใช้การควบคุม PID บทความนี้ได้รับการพัฒนาโดยให้การแนะนำสั้น ๆ เกี่ยวกับระบบควบคุมและคำศัพท์ที่เกี่ยวข้อง นอกเหนือจากแรงจูงใจสำหรับโครงการ ได้มีการทดลองและสังเกต ข้อดีและข้อเสียที่อธิบายโดยสิ้นสุดที่การปรับปรุงในอนาคต หุ่นจำลองการทรงตัวในตัวเองได้รับการพัฒนาขึ้นเพื่อให้เข้าใจถึงประสิทธิภาพของ PID ในโลกของระบบควบคุม เมื่อผ่านการทดสอบและทดลองอย่างเข้มงวด ข้อดีและข้อเสียของระบบควบคุม PID ถูกค้นพบ พบว่าแม้จะมีข้อดีหลายประการของการควบคุม PID เหนือวิธีการที่ผ่านมา แต่ระบบนี้ยังต้องปรับปรุงอีกมาก หวังว่าผู้อ่านจะเข้าใจถึงความสำคัญของการสร้างสมดุลในตนเอง ประสิทธิภาพ และข้อบกพร่องของการควบคุม PID

ขั้นตอนที่ 1: บทนำ

ด้วยการถือกำเนิดของคอมพิวเตอร์และกระบวนการทางอุตสาหกรรม ตลอดประวัติศาสตร์ของมนุษย์ มีการวิจัยเพื่อพัฒนาวิธีการปรับแต่งกระบวนการอยู่เสมอ และที่สำคัญกว่านั้นคือ การควบคุมพวกเขาโดยใช้เครื่องจักรโดยอัตโนมัติ มีวัตถุประสงค์เพื่อลดการมีส่วนร่วมของมนุษย์ในกระบวนการเหล่านี้ ซึ่งจะช่วยลดข้อผิดพลาดในกระบวนการเหล่านี้ จึงได้พัฒนาสาขา”วิศวกรรมระบบควบคุม” วิศวกรรมระบบควบคุมสามารถกำหนดได้โดยใช้วิธีการต่างๆ เพื่อควบคุมการทำงานของกระบวนการหรือการบำรุงรักษาสภาพแวดล้อมที่คงที่และเป็นที่ต้องการ ไม่ว่าจะเป็นแบบแมนนวลหรือแบบอัตโนมัติ

ตัวอย่างง่ายๆ เช่น การควบคุมอุณหภูมิในห้อง การควบคุมด้วยตนเอง หมายถึงการมีอยู่ของบุคคลในไซต์ที่ตรวจสอบสภาพปัจจุบัน (เซ็นเซอร์) เปรียบเทียบกับค่าที่ต้องการ (การประมวลผล) และดำเนินการตามความเหมาะสมเพื่อให้ได้ค่าที่ต้องการ (ตัวกระตุ้น) ปัญหาของวิธีนี้คือไม่น่าเชื่อถือนักเนื่องจากบุคคลมักมีข้อผิดพลาดหรือประมาทเลินเล่อในการทำงาน นอกจากนี้ ปัญหาอีกประการหนึ่งคืออัตราของกระบวนการที่เริ่มต้นโดยแอคทูเอเตอร์นั้นไม่สม่ำเสมอเสมอไป ซึ่งหมายความว่าบางครั้งอาจเกิดขึ้นเร็วกว่าที่กำหนดหรือบางครั้งอาจช้า การแก้ปัญหานี้คือการใช้ไมโครคอนโทรลเลอร์เพื่อควบคุมระบบ ไมโครคอนโทรลเลอร์คือ

โปรแกรมควบคุมกระบวนการตามข้อกำหนดที่กำหนดซึ่งเชื่อมต่อในวงจร (จะกล่าวถึงในภายหลัง) ป้อนค่าหรือเงื่อนไขที่ต้องการและด้วยเหตุนี้จึงควบคุมกระบวนการเพื่อรักษาค่าที่ต้องการ ข้อดีของกระบวนการนี้คือไม่ต้องมีการแทรกแซงของมนุษย์ในกระบวนการนี้ นอกจากนี้อัตราของกระบวนการยังสม่ำเสมอ

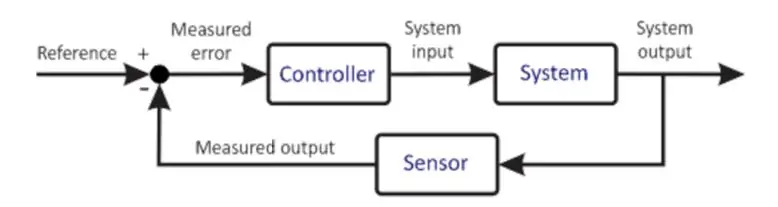
ระบบควบคุมพื้นฐาน

ไดอะแกรมก่อนหน้านี้แสดงเวอร์ชันที่ง่ายมากของระบบควบคุม ไมโครคอนโทรลเลอร์คือหัวใจของระบบควบคุมใดๆ เป็นองค์ประกอบที่สำคัญมาก ดังนั้น การเลือกควรทำอย่างระมัดระวังตามข้อกำหนดของระบบ ไมโครคอนโทรลเลอร์รับอินพุตจากผู้ใช้ อินพุตนี้กำหนดเงื่อนไขที่ต้องการของระบบ ไมโครคอนโทรลเลอร์ยังได้รับอินพุตป้อนกลับจากเซ็นเซอร์ เซ็นเซอร์นี้เชื่อมต่อกับเอาต์พุตของระบบ ซึ่งข้อมูลจะถูกป้อนกลับไปยังอินพุต ไมโครโปรเซสเซอร์ที่อิงจากการเขียนโปรแกรม ทำการคำนวณต่างๆ และให้เอาต์พุตไปยังแอคทูเอเตอร์ แอคทูเอเตอร์จะควบคุมโรงงานให้พยายามรักษาสภาพเหล่านั้นโดยยึดตามเอาต์พุต ตัวอย่างอาจเป็นตัวขับมอเตอร์ที่ขับมอเตอร์โดยที่ตัวขับมอเตอร์เป็นตัวกระตุ้นและมอเตอร์คือโรงงาน มอเตอร์จึงหมุนด้วยความเร็วที่กำหนด เซ็นเซอร์ที่เชื่อมต่อจะอ่านสภาพของโรงงานในขณะนั้นและป้อนกลับไปยังไมโครคอนโทรลเลอร์ ไมโครคอนโทรลเลอร์ทำการเปรียบเทียบอีกครั้ง ทำการคำนวณ และด้วยเหตุนี้ วัฏจักรจึงทำซ้ำตัวเอง กระบวนการนี้ซ้ำซากและไม่มีที่สิ้นสุดโดยไมโครคอนโทรลเลอร์จะรักษาสภาวะที่ต้องการ

ขั้นตอนที่ 2: ระบบควบคุมด้วย PID

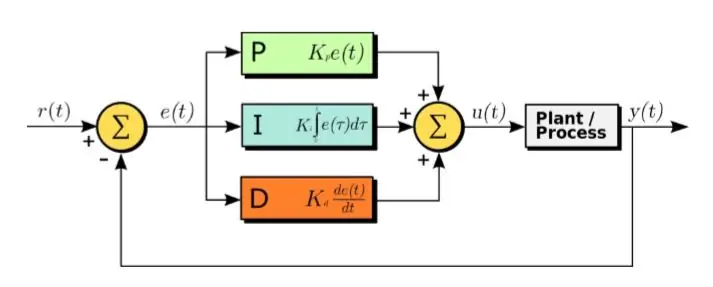
อัลกอริทึม PID เป็นวิธีการที่มีประสิทธิภาพในการออกแบบระบบควบคุม

คำนิยาม

PID ย่อมาจาก Proportional, Integral และ Derivative ในอัลกอริธึมนี้ สัญญาณผิดพลาดที่ได้รับคืออินพุต และสมการต่อไปนี้ใช้กับสัญญาณผิดพลาด

U(t) = Kp∗e(t) + Kd∗d/dt(e(t)) + Ki∗integral(e(t)) (1.1)

คำอธิบายโดยย่อ

ดังที่เห็นได้ในสมการข้างต้น อินทิกรัลและอนุพันธ์ของสัญญาณผิดพลาดจะถูกคำนวณ คูณด้วยค่าคงที่ตามลำดับและบวกเข้ากับค่าคงที่ Kp คูณด้วย e(t) เอาต์พุตจะถูกส่งไปยังแอคทูเอเตอร์ซึ่งทำให้ระบบทำงาน ทีนี้มาดูแต่ละส่วนของฟังก์ชั่นกัน ฟังก์ชันนี้ส่งผลต่อเวลาขึ้น เวลาตก เวลาสูงสุดในการถ่ายภาพ เวลาตกตะกอน และข้อผิดพลาดของสภาวะคงตัวโดยตรง

• ส่วนตามสัดส่วน: ส่วนที่เป็นสัดส่วนช่วยลดเวลาการขึ้นและลดข้อผิดพลาดของสถานะคงตัว ซึ่งหมายความว่าระบบจะใช้เวลาน้อยกว่าในการเข้าถึงค่าสูงสุด และเมื่อถึงสถานะคงตัว ข้อผิดพลาดของสถานะคงตัวจะต่ำ อย่างไรก็ตาม มันเพิ่มยอดเกิน

• ส่วนอนุพันธ์: ส่วนอนุพันธ์จะลดระยะเวลาที่เกินและเวลาในการตกตะกอน ซึ่งหมายความว่าสถานะชั่วคราวของระบบจะลดลงมากขึ้น นอกจากนี้ระบบจะเข้าสู่สถานะคงตัวในเวลาที่น้อยลง อย่างไรก็ตาม ไม่มีผลใด ๆ เกี่ยวกับเวลาเพิ่มขึ้นหรือข้อผิดพลาดของสถานะคงตัว

• ส่วนประกอบสำคัญ: ส่วนประกอบสำคัญช่วยลดเวลาการขึ้นลงและขจัดข้อผิดพลาดในสภาวะคงตัวได้อย่างสมบูรณ์ อย่างไรก็ตาม จะเพิ่มการโอเวอร์ชูตสูงสุดและเวลาการตกตะกอน

• การปรับจูน: ระบบควบคุมที่ดีจะมีเวลาต่ำ เวลาตกตะกอน ยอดเกิน และข้อผิดพลาดสถานะคงตัว ดังนั้นจึงต้องปรับ Kp, Kd, Ki อย่างละเอียดเพื่อปรับการมีส่วนร่วมของปัจจัยข้างต้นเพื่อให้ได้ระบบควบคุมที่ดี

แนบรูปภาพที่แสดงผลกระทบของการเปลี่ยนแปลงพารามิเตอร์ต่างๆ ในอัลกอริธึม PID

ขั้นตอนที่ 3: หุ่นยนต์ปรับสมดุลตนเอง

หุ่นยนต์ทรงตัวเป็นหุ่นยนต์สองล้อหลายชั้น

หุ่นยนต์จะพยายามทำให้ตัวเองสมดุลกับการใช้แรงที่ไม่เท่ากัน มันจะสร้างสมดุลโดยการใช้แรงต่อต้านผลลัพธ์ของแรงที่กระทำต่อหุ่นยนต์

วิธีการปรับสมดุลตนเอง

มีสี่วิธีในการปรับสมดุลตนเองของหุ่นยนต์ เหล่านี้มีดังนี้:

ปรับสมดุลตัวเองโดยใช้ IR Tilt Sensor สองตัว

นี่เป็นวิธีหนึ่งที่หยาบคายที่สุดในการปรับสมดุลหุ่นยนต์ เนื่องจากต้องใช้ฮาร์ดแวร์น้อยกว่ามากและอัลกอริธึมที่ค่อนข้างง่าย ในแนวทางนี้ เซ็นเซอร์ IR แบบเอียงสองตัวถูกใช้เพื่อวัดระยะห่างระหว่างพื้นดินกับหุ่นยนต์ ตามระยะทางที่คำนวณได้ สามารถใช้ PID เพื่อขับเคลื่อนมอเตอร์เพื่อให้สมดุลกับหุ่นยนต์ได้ ข้อเสียอย่างหนึ่งของวิธีนี้คือเซ็นเซอร์ IR อาจพลาดการอ่านค่าบางส่วน ปัญหาอีกประการหนึ่งคือต้องใช้อินเทอร์รัปต์และลูปในการคำนวณระยะทางซึ่งเพิ่มความซับซ้อนของเวลาของอัลกอริธึม ดังนั้น วิธีการสร้างสมดุลของหุ่นยนต์จึงไม่ค่อยมีประสิทธิภาพมากนัก

ปรับสมดุลตนเองโดยใช้มาตรความเร่ง

มาตรความเร่งทำให้เรามีความเร่งของร่างกายใน 3 แกน การเร่งความเร็วในแกน y (ขึ้นไป) และแกน x (ไปข้างหน้า) ทำให้เรามีการวัดเพื่อคำนวณทิศทางของแรงโน้มถ่วงและด้วยเหตุนี้จึงคำนวณมุมเอียง มุมคำนวณดังนี้:

θ = arctan(Ay/ขวาน) (1.2)

ข้อเสียของการใช้วิธีนี้คือระหว่างการเคลื่อนที่ของหุ่นยนต์ ความเร่งในแนวนอนจะถูกเพิ่มเข้าไปในการอ่านซึ่งเป็นสัญญาณรบกวนความถี่สูง ดังนั้นมุมเอียงจะคลาดเคลื่อน

การทรงตัวโดยใช้ไจโรสโคป

ไจโรสโคปใช้ในการคำนวณความเร็วเชิงมุมตามแกนทั้งสาม มุมเอียงได้มาจากสมการต่อไปนี้

θp(i) = θp(i-1) + 1/6(vali-3 + 2vali−2 + 2vali-1 + วาลี่) (1.3)

ข้อเสียใหญ่ประการหนึ่งของการใช้ไจโรสโคปคือมี DC Bias ขนาดเล็กซึ่งเป็นสัญญาณรบกวนความถี่ต่ำ และในบางครั้ง ค่าที่ส่งกลับจะผิดพลาดโดยสิ้นเชิง เมื่อรวมเข้าด้วยกันแล้วจะทำให้จุดศูนย์หายไป ด้วยเหตุนี้ หุ่นยนต์จะยังคงอยู่ในตำแหน่งแนวตั้งเป็นระยะเวลาหนึ่งและจะล้มลงเมื่อการดริฟท์มาถึง

ปรับสมดุลตัวเองโดยใช้ทั้งมาตรความเร่งและไจโรสโคป

ตามที่กล่าวไว้ข้างต้น การใช้เฉพาะมาตรความเร่งหรือไจโรสโคปจะไม่ให้มุมเอียงที่ถูกต้องแก่เรา เพื่อพิจารณาว่าจะใช้ทั้งมาตรความเร่งและไจโรสโคป ทั้งสองอย่างนี้ฝังอยู่ใน MPU6050 ในที่นี้ เราได้รับข้อมูลจากทั้งคู่แล้วรวมเข้าด้วยกันโดยใช้ตัวกรองคาลมานหรือตัวกรองเสริม

• ตัวกรองคาลมาน: ตัวกรองคาลมานคำนวณค่าประมาณที่ดีที่สุดของสถานะของระบบไดนามิกจากการวัดที่มีสัญญาณรบกวน ลดความคลาดเคลื่อนกำลังสองเฉลี่ยของการประมาณการ มันทำงานในสองขั้นตอน การทำนายและการแก้ไข โดยให้สมการสุ่มแบบไม่ต่อเนื่องที่อธิบายไดนามิกของระบบ อย่างไรก็ตาม เป็นอัลกอริธึมที่ซับซ้อนมากในการใช้งานโดยเฉพาะกับฮาร์ดแวร์ที่จำกัดของไมโครคอนโทรลเลอร์

• ตัวกรองเสริม: อัลกอริธึมนี้ใช้ข้อมูลที่ได้จากไจโรสโคปเป็นหลักและรวมเข้าด้วยกันเมื่อเวลาผ่านไปเพื่อให้ได้มุมเอียง นอกจากนี้ยังใช้การอ่านค่าความเร่งในสัดส่วนเพียงเล็กน้อย ตัวกรองเสริมช่วยลดสัญญาณรบกวนความถี่สูงของมาตรความเร่งและสัญญาณรบกวนความถี่ต่ำของไจโรสโคป จากนั้นหลอมรวมเพื่อให้ได้มุมเอียงที่แม่นยำที่สุด

ขั้นตอนที่ 4: การออกแบบหุ่นยนต์

เราได้ออกแบบหุ่นยนต์ทรงตัวโดยใช้ตัวควบคุม Proportional Derivative ที่ดำเนินการโดย Complementary Filter สำหรับ MPU6050 หุ่นยนต์ Self Balancing รุ่นเล็กนี้จะแสดงให้เห็นประโยชน์ของระบบควบคุมในการปรับสมดุลตนเองของหุ่นยนต์

การใช้งานระบบ:

ระบบนี้เป็นหุ่นยนต์ทรงตัว มันถูกใช้งานโดยใช้ PID Controller ซึ่งเป็น Proportional Integral Derivative Controller เราสร้างสมดุลให้หุ่นยนต์ด้วยการขับล้อไปในทิศทางที่ตกลงมา ในการทำเช่นนั้น เรากำลังพยายามรักษาจุดศูนย์ถ่วงของหุ่นยนต์ให้อยู่เหนือจุดหมุน ในการขับเคลื่อนล้อไปในทิศทางที่มันตกลงมา เราควรรู้ว่าหุ่นยนต์กำลังตกลงมาที่ไหนและความเร็วที่มันตกลงมา ข้อมูลนี้ได้มาจากการใช้ MPU6050 ซึ่งมีมาตรความเร่งและไจโรสโคป MPU6050 วัดมุมเอียงและส่งออกไปยังไมโครคอนโทรลเลอร์ MPU6050 เชื่อมต่อกับบอร์ด STM ผ่าน I2C ใน I2C สายหนึ่งใช้สำหรับนาฬิกาซึ่งมีชื่อว่า SCL อีกอันหนึ่งสำหรับการถ่ายโอนข้อมูลซึ่งก็คือ SDA ในนี้จะใช้การสื่อสารมาสเตอร์ทาส ที่อยู่เริ่มต้นและที่อยู่สิ้นสุดได้รับการระบุเพื่อให้ทราบว่าข้อมูลเริ่มต้นจากที่ใดและสิ้นสุดที่ใด เราได้นำ Complementary Filter มาใช้ที่นี่สำหรับ MPU6050 ซึ่งเป็นตัวกรองคณิตศาสตร์เพื่อรวมเอาท์พุตของมาตรความเร่งและไจโรสโคป หลังจากได้รับข้อมูลจาก MPU6050 แล้ว ไมโครคอนโทรลเลอร์จะทำการคำนวณเพื่อทราบว่าตกอยู่ที่ใด จากการคำนวณ ไมโครคอนโทรลเลอร์ STM จะให้คำสั่งกับคนขับมอเตอร์ให้ขับยานพาหนะไปในทิศทางที่ตกลงมา ซึ่งจะทำให้หุ่นยนต์สมดุล

ขั้นตอนที่ 5: ส่วนประกอบของโครงการ

ส่วนประกอบต่อไปนี้ถูกใช้ในโครงการหุ่นยนต์ปรับสมดุลตัวเอง:

STM32F407

ไมโครคอนโทรลเลอร์ที่ออกแบบโดย ST Microelectronics ทำงานบนสถาปัตยกรรม ARM Cortex-M

ตัวขับมอเตอร์ L298N

IC นี้ใช้สำหรับการสั่งงานมอเตอร์ ได้รับสองอินพุตภายนอก หนึ่งจากไมโครคอนโทรลเลอร์ที่ส่งสัญญาณ PWM โดยการปรับความกว้างของพัลส์ สามารถปรับความเร็วของมอเตอร์ได้ อินพุตที่สองคือแหล่งจ่ายแรงดันไฟฟ้าที่จำเป็นสำหรับการขับเคลื่อนมอเตอร์ซึ่งเป็นแบตเตอรี่ 12V ในกรณีของเรา

มอเตอร์กระแสตรง

มอเตอร์กระแสตรงทำงานบนแหล่งจ่ายกระแสตรง ในการทดลองนี้ มอเตอร์กระแสตรงกำลังทำงานโดยใช้ออปโตคัปเปลอร์ที่เชื่อมต่อกับตัวขับมอเตอร์ ในการขับเคลื่อนมอเตอร์ เราใช้ Motor Drive L298N

MPU6050

MPU6050 ใช้เพื่อรับข้อมูลเกี่ยวกับตำแหน่งที่หุ่นยนต์ตกลงมา มันวัดมุมเอียงเทียบกับจุดเอียงศูนย์ซึ่งเป็นตำแหน่งของ MPU6050 เมื่อโปรแกรมเริ่มทำงาน

MPU6050 มีมาตรความเร่งแบบ 3 แกนและไจโรสโคปแบบ 3 แกน มาตรความเร่งจะวัดความเร่งตามแกนทั้งสาม และไจโรสโคปจะวัดอัตราเชิงมุมของแกนทั้งสาม ในการรวมเอาท์พุต เราต้องกรองสัญญาณรบกวนของทั้งคู่ออก ในการกรองเสียงรบกวน เรามีตัวกรอง Kalman และ Complementary เราได้นำตัวกรองเสริมมาใช้ในโครงการของเรา

ออปโต้คู่รัก 4N35

ออปโตคัปเปลอร์เป็นอุปกรณ์ที่ใช้ในการแยกส่วนแรงดันต่ำและส่วนแรงดันสูงของวงจร ตามชื่อของมัน มันทำงานโดยใช้แสงเป็นหลัก เมื่อส่วนแรงดันต่ำได้รับสัญญาณ กระแสจะไหลในส่วนไฟฟ้าแรงสูง

ขั้นตอนที่ 6: โครงสร้างของหุ่นยนต์

อธิบายโครงสร้างของหุ่นยนต์ได้ดังนี้

โครงสร้างทางกายภาพ

หุ่นยนต์ทรงตัวประกอบด้วยสองชั้นที่ประกอบด้วยแก้วพลาสติกใส รายละเอียดของสองชั้นได้รับด้านล่าง:

ชั้นแรก

ในส่วนล่างสุดของเลเยอร์แรก เราได้วางเซลล์เพื่อจ่ายไฟให้กับบอร์ด STM นอกจากนี้ยังมีการวางมอเตอร์สองตัวขนาด 4 โวลต์ไว้ในแต่ละด้านโดยมียางที่เชื่อมต่อเพื่อให้หุ่นยนต์เคลื่อนที่ได้ ในส่วนบนของชั้นแรก มีการวางแบตเตอรี่สองก้อนก้อนละ 4 โวลต์ (รวมทั้งหมด 8 โวลต์) และ IC ขับมอเตอร์ (L298N) สำหรับการทำงานของมอเตอร์

ชั้นที่สอง

ในชั้นบนของหุ่นยนต์ เราได้วางบอร์ด STM ไว้บนบอร์ดประสิทธิภาพ บอร์ดที่สมบูรณ์แบบของออปโตคัปปลิ้ง 4 อันวางอยู่บนชั้นบนสุด ไจโรสโคปยังถูกวางไว้ที่ชั้นบนสุดของหุ่นยนต์จากด้านล่าง ส่วนประกอบทั้งสองวางอยู่ตรงกลางเพื่อให้จุดศูนย์ถ่วงอยู่ต่ำที่สุด

จุดศูนย์ถ่วงของหุ่นยนต์

จุดศูนย์ถ่วงถูกรักษาให้ต่ำที่สุด เพื่อจุดประสงค์นี้ เราได้วางแบตเตอรี่ขนาดใหญ่ไว้ที่ชั้นล่างและส่วนประกอบที่เบา เช่น บอร์ด STM และออปโตคัปเปลอร์ที่ชั้นบน

ขั้นตอนที่ 7: รหัส

รหัสถูกรวบรวมบน Atolic TrueStudio STM studio ถูกใช้เพื่อจุดประสงค์ในการดีบัก

ขั้นตอนที่ 8: สรุป

หลังจากการทดลองและการสังเกตเป็นจำนวนมาก ในที่สุดเราก็มาถึงจุดที่เราสรุปผลของเราและอภิปรายว่าเราประสบความสำเร็จในการดำเนินการและหาประสิทธิภาพของระบบมากน้อยเพียงใด

รีวิวทั่วไป

ในระหว่างการทดลอง สามารถควบคุมความเร็วของมอเตอร์ได้สำเร็จโดยใช้อัลกอริทึม PID อย่างไรก็ตาม เส้นโค้งไม่ได้เป็นเส้นตรงเรียบ มีเหตุผลหลายประการสำหรับสิ่งนั้น:

• เซ็นเซอร์แม้ว่าจะเชื่อมต่อกับฟิลเตอร์กรองความถี่ต่ำยังคงให้การยุบตัวที่แน่นอน; สิ่งเหล่านี้เกิดจากความต้านทานที่ไม่ใช่เชิงเส้นและสาเหตุที่หลีกเลี่ยงไม่ได้ของอุปกรณ์อิเล็กทรอนิกส์แบบแอนะล็อก

• มอเตอร์ไม่หมุนอย่างราบรื่นภายใต้แรงดันไฟฟ้าขนาดเล็กหรือ PWM มันทำให้เกิดการกระตุกที่อาจทำให้ค่าผิดบางอย่างถูกป้อนเข้าสู่ระบบ

• เนื่องจากการโยกเยก เซ็นเซอร์อาจพลาดช่องบางช่องที่ให้ค่าที่สูงกว่า • สาเหตุหลักอีกประการของข้อผิดพลาดอาจเป็นความถี่สัญญาณนาฬิกาหลักของไมโครคอนโทรลเลอร์ STM ไมโครคอนโทรลเลอร์ STM รุ่นนี้มีนาฬิกาหลักที่ 168MHz แม้ว่าจะจัดการกับปัญหานี้ในโครงการนี้ แต่ก็มีแนวคิดโดยรวมเกี่ยวกับโมเดลนี้ว่าไม่มีความถี่สูงเช่นนั้นอย่างแน่นอน

ความเร็วของลูปเปิดทำให้เส้นเรียบมากโดยมีค่าที่ไม่คาดคิดเพียงไม่กี่ค่า อัลกอริธึม PID ยังทำงานได้ดีทำให้มอเตอร์มีเวลาการตกตะกอนต่ำมาก อัลกอริธึม PID ของมอเตอร์ได้รับการทดสอบภายใต้แรงดันไฟฟ้าต่างๆ โดยรักษาความเร็วอ้างอิงให้คงที่ การเปลี่ยนแปลงของแรงดันไฟฟ้าไม่เปลี่ยนความเร็วของมอเตอร์ซึ่งแสดงว่าอัลกอริธึม PID ทำงานได้ดี

ประสิทธิภาพ

ในที่นี้เราจะพูดถึงประสิทธิภาพของตัวควบคุม PID ที่เราสังเกตเห็นระหว่างการทดลอง

การใช้งานอย่างง่าย

เราได้เห็นในส่วนการทดลองและการสังเกตแล้วว่าตัวควบคุม PID นั้นใช้งานง่ายมาก ต้องการเพียงสามพารามิเตอร์หรือค่าคงที่ที่ต้องตั้งค่าเพื่อให้มีระบบควบคุมความเร็ว

ประสิทธิภาพที่เหนือกว่าสำหรับระบบเชิงเส้นตรง

ตัวควบคุม Linear PID มีประสิทธิภาพมากที่สุดในตระกูลตัวควบคุม เนื่องจากตรรกะนั้นง่ายมากและแอปพลิเคชันแพร่หลายในกรณีที่แอปพลิเคชันเชิงเส้นหรือค่อนข้างเชิงเส้น

ข้อจำกัด

เราได้อธิบายไว้ในบทคัดย่อเกี่ยวกับข้อจำกัดของระบบนี้ ที่นี่เราพูดถึงบางส่วนที่เราสังเกตเห็น

การเลือกค่าคงที่

เราได้เห็นแล้วว่าแม้ว่าตัวควบคุม PID จะใช้งานง่าย แต่ก็ยังเป็นข้อเสียเปรียบที่สำคัญของระบบที่ขั้นตอนในการเลือกค่าของค่าคงที่นั้นค่อนข้างลำบาก เพราะต้องทำการคำนวณแบบผิดๆ อีกวิธีหนึ่งคือวิธีตีและทดลอง แต่ก็ไม่มีประสิทธิภาพเช่นกัน

ค่าคงที่ไม่คงที่เสมอไป

ผลการทดลองแสดงให้เห็นว่าสำหรับค่าต่าง ๆ ของความเร็วอ้างอิงสำหรับมอเตอร์ ตัวควบคุม PID ทำงานผิดปกติสำหรับค่าคงที่ PID เดียวกัน สำหรับความเร็วที่ต่างกัน จะต้องเลือกค่าคงที่แบบต่างๆ กัน ซึ่งจะทำให้ต้นทุนการคำนวณเพิ่มขึ้นแบบทวีคูณ

ไม่ใช่เชิงเส้น

ตัวควบคุม PID ที่ใช้ในกรณีของเราเป็นแบบเชิงเส้น ดังนั้นจึงใช้ได้กับระบบเชิงเส้นตรงเท่านั้น สำหรับระบบที่ไม่เป็นเชิงเส้น ตัวควบคุมจะต้องถูกใช้งานอย่างหลากหลาย แม้ว่าจะมีวิธี PID ที่ไม่ใช่เชิงเส้นที่แตกต่างกัน แต่ก็ต้องมีการเลือกพารามิเตอร์เพิ่มเติม สิ่งนี้ทำให้ระบบไม่เป็นที่พึงปรารถนาอีกครั้งเนื่องจากมีต้นทุนในการคำนวณสูง

ต้องกดเริ่มต้น

เราแสดงให้เห็นในส่วนการทดลองว่าสำหรับความเร็วอ้างอิงที่ค่อนข้างเล็กซึ่งข้อผิดพลาดค่อนข้างเล็กในการสตาร์ท PWM ที่จัดหาโดย PID นั้นเล็กมากจนไม่สร้างแรงบิดเริ่มต้นที่จำเป็นสำหรับมอเตอร์ ดังนั้น มอเตอร์ในรุ่นทดลองบางรุ่นไม่ทำงาน หรือในรุ่นทดลองอื่นๆ ให้ค่าโอเวอร์ชูตที่มากและใช้เวลานานขึ้น

ขั้นตอนที่ 9: ขอขอบคุณเป็นพิเศษ

ขอขอบคุณเป็นพิเศษกับสมาชิกในกลุ่มที่ช่วยฉันผ่านโครงการนี้

ฉันจะอัปโหลดลิงค์ไปยังวิดีโอเร็ว ๆ นี้

ฉันหวังว่าคุณจะพบว่าคำแนะนำนี้น่าสนใจ

นี่คือ Tahir Ul Haq จาก UET ลงนาม ไชโย !!!