☠WEEDINATOR☠ ตอนที่ 4: รหัสเรขาคณิตการบังคับเลี้ยวแบบเฟืองท้าย: 3 ขั้นตอน

2024 ผู้เขียน: John Day | [email protected]. แก้ไขล่าสุด: 2024-01-30 13:07

หากคุณมีเวลารับชมวิดีโอด้านบน คุณจะสังเกตเห็นว่ามีเสียงแปลกๆ เกิดขึ้นจากมอเตอร์ที่พวงมาลัยหยุดนิ่งเป็นระยะๆ ขณะที่ WEEDINATOR นำทางด้วยการเลี้ยว 3 จุด มอเตอร์มักจะติดขัดซึ่งกันและกัน เนื่องจากรัศมีการเลี้ยวจากด้านในออกด้านนอกต่างกัน และระยะทางที่ล้อเคลื่อนที่จะแตกต่างกันไปตามระดับการเลี้ยว

เรขาคณิตของทางเลี้ยวสามารถทำได้โดยร่างการเรียงสับเปลี่ยนของทางเลี้ยว 8 ครั้งหรือมากกว่านั้น โดยยกตัวอย่างการเลี้ยวในมุมต่างๆ ของวงล้อด้านในตั้งแต่ 0 (ไม่มีการหมุน) ถึง 90 (ล็อกเต็ม) องศา ฟังดูซับซ้อน?

หุ่นยนต์ล้อขนาดเล็กส่วนใหญ่ไม่พยายามบังคับเลี้ยวที่ซับซ้อนใดๆ และพึ่งพาเพียงแค่การเปลี่ยนความเร็วสัมพัทธ์ของมอเตอร์ในแต่ละด้านของรถ อย่างมีประสิทธิภาพ ซึ่งค่อนข้างจะเหมือนกับรถขุดหรือรถถังที่ถูกติดตาม ทำงาน นี่เป็นสิ่งที่ดีถ้าคุณกำลังชาร์จเหนือเขตสงครามที่เต็มไปด้วยปล่องยิงทุกอย่างที่เคลื่อนที่ แต่ในสภาพแวดล้อมทางการเกษตรที่เงียบสงบ สิ่งสำคัญคือต้องสร้างความเสียหายให้น้อยที่สุดกับดินและพื้นดินให้มากที่สุดเท่าที่จะเป็นไปได้ ดังนั้นการบดล้อไปมาระหว่างกัน ไม่เหมาะสม!

รถยนต์และรถแทรกเตอร์ส่วนใหญ่มีอุปกรณ์ที่มีประโยชน์มากที่เรียกว่า 'Differential' ยกเว้นรถที่คุณเห็นในภาพยนตร์อเมริกันสมัยก่อน ซึ่งคุณจะได้ยินเสียงยางร้องอย่างบ้าคลั่งทุกครั้งที่เข้าโค้ง ชาวอเมริกันยังคงสร้างรถยนต์แบบนี้หรือไม่? ด้วย WEEDINATOR เราสามารถตั้งโปรแกรมส่วนต่างในมอเตอร์ขับเคลื่อนโดยคำนวณสูตรสำหรับความเร็วสัมพัทธ์และมุมของล้อที่มุมการเลี้ยวเฉพาะ ยังฟังดูซับซ้อน?

นี่คือตัวอย่างด่วน:

หาก WEEDINATOR กำลังนำทางและมีวงล้อด้านในที่ 45 องศา ล้อด้านนอกจะไม่เท่ากับ 45 องศา เท่ากับ 30 องศามากกว่า นอกจากนี้ ล้อด้านในอาจหมุนได้ 1 กม./ชม. แต่ล้อด้านนอกจะเร็วขึ้นอย่างมาก เช่น 1.35 กม./ชม.

ขั้นตอนที่ 1: การตั้งค่าเรขาคณิต

มีการตั้งสมมติฐานพื้นฐานสองสามข้อเพื่อเริ่มต้นด้วย:

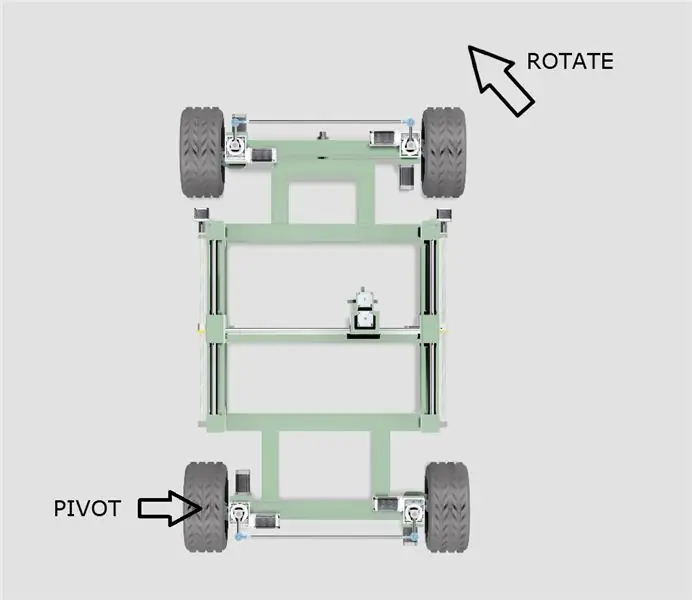
• แชสซีจะหมุนรอบล้อหลังหนึ่งล้อดังแสดงในแผนภาพด้านบน
• ศูนย์กลางที่มีประสิทธิภาพของวงกลมเดือยจะเคลื่อนที่ไปตามเส้นที่ยื่นออกมาจากศูนย์กลางของล้อหลังทั้งสอง ขึ้นอยู่กับมุมของการเลี้ยว
• เรขาคณิตจะอยู่ในรูปของเส้นโค้งไซน์

ขั้นตอนที่ 2: ภาพวาดที่ปรับขนาดของมุมล้อและรัศมี

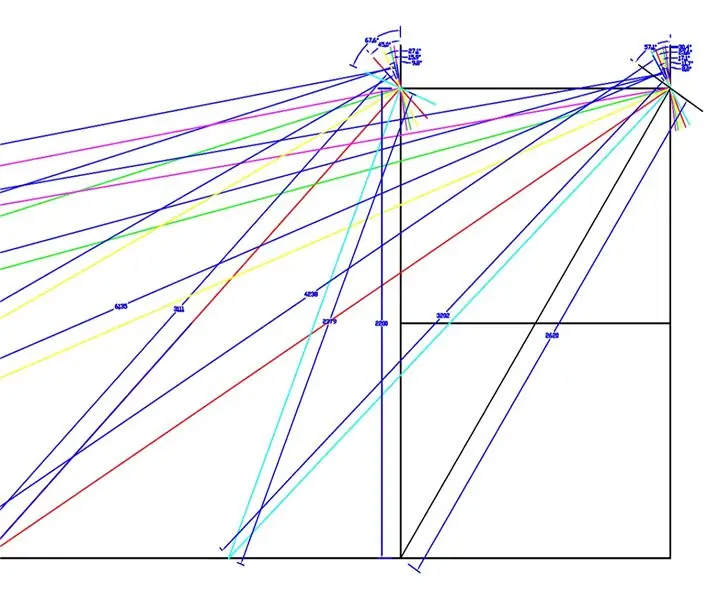
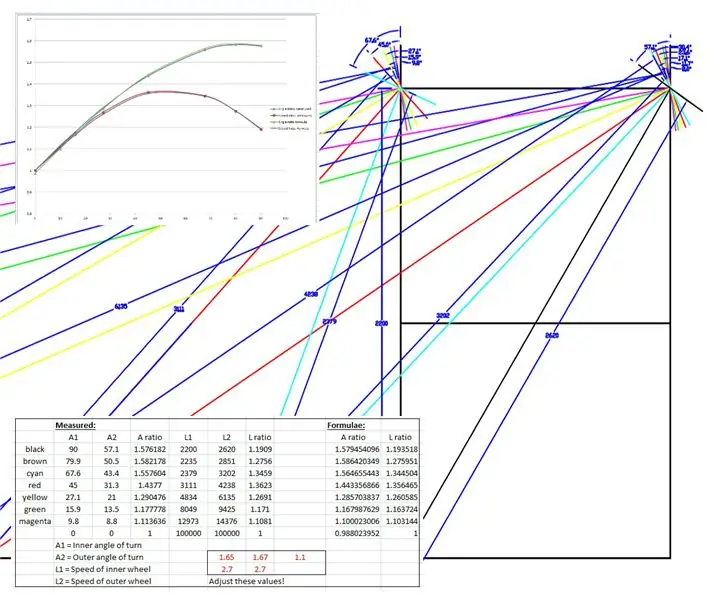
ภาพวาดแบบเต็มสเกลทำจากล้อหน้าและแชสซีของ WEEDINATOR โดยมีการเรียงสับเปลี่ยนกันของมุมล้อภายใน 8 แบบระหว่าง 0 ถึง 90 องศา และศูนย์เลี้ยวตามลำดับนั้นได้รับการแมปตามที่แสดงในภาพวาดด้านบน

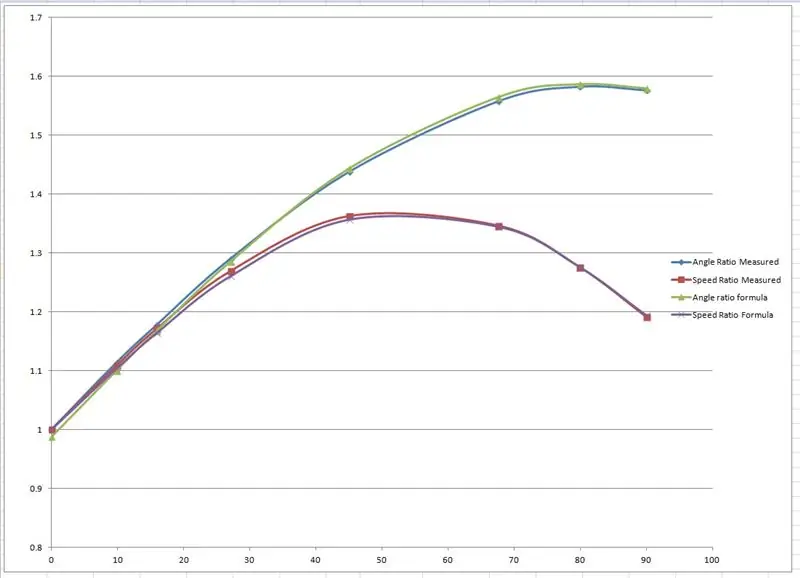
รัศมีมีผลวัดจากการวาดและลงจุดบนกราฟใน Microsoft Excel

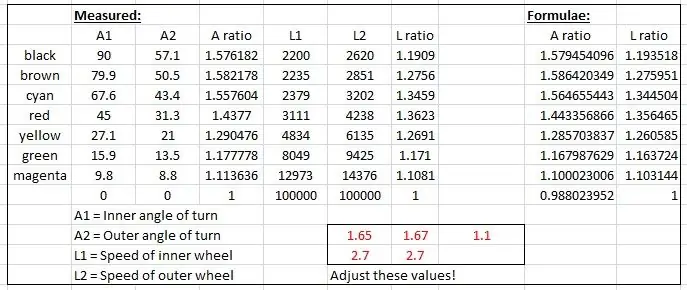
มีการสร้างกราฟสองกราฟ อันหนึ่งเป็นอัตราส่วนของเพลาล้อหน้าซ้ายและขวา และอีกอันสำหรับอัตราส่วนของรัศมีสองอันสำหรับมุมเลี้ยวแต่ละอัน

จากนั้นฉันก็ 'เหลวไหล' สูตรบางอย่างเพื่อเลียนแบบผลลัพธ์เชิงประจักษ์โดยอิงจากเส้นโค้งไซน์ ฟัดจ์ตัวใดตัวหนึ่งมีลักษณะดังนี้:

speedRatio= (บาป(ภายใน*1.65*pi/180)+2.7)/2.7; // ด้านในคือมุมเลี้ยวด้านใน

เส้นโค้งถูกทำให้เหลวไหลโดยการเปลี่ยนค่าที่แสดงเป็นสีแดงในไฟล์ excel จนกว่าส่วนโค้งจะพอดีกัน

ขั้นตอนที่ 3: การเข้ารหัสสูตร

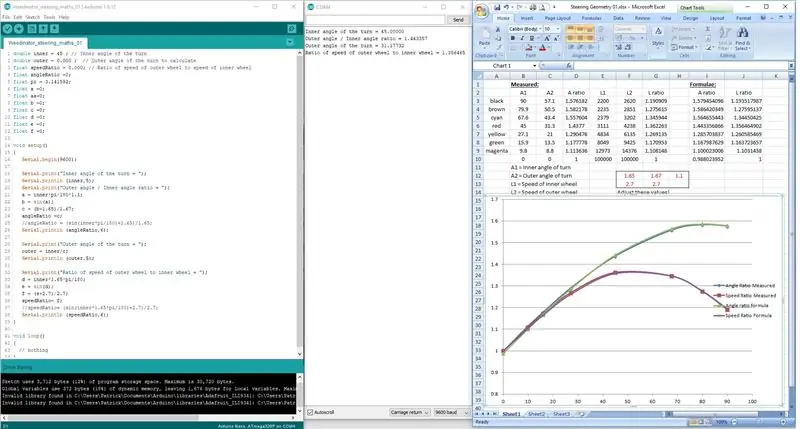
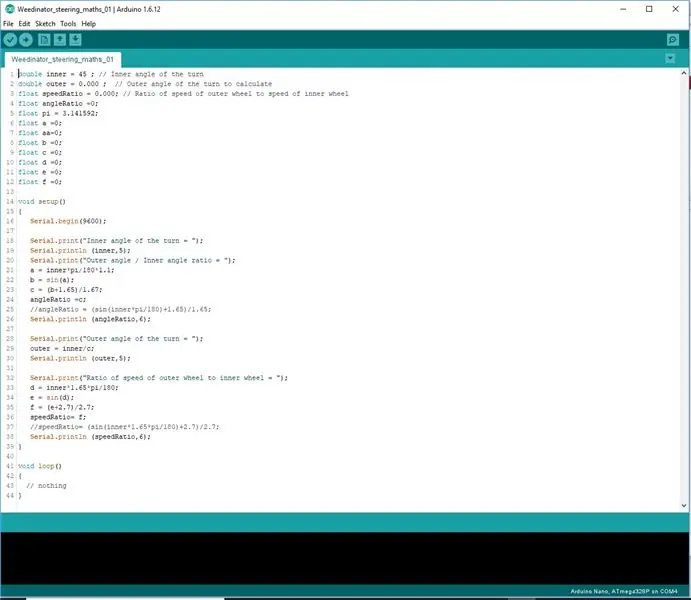
แทนที่จะพยายามเขียนโค้ดสูตรในบรรทัดเดียว พวกเขาแบ่งออกเป็น 3 ขั้นตอนเพื่อให้ Arduino สามารถประมวลผลทางคณิตศาสตร์ได้อย่างถูกต้อง

ผลลัพธ์จะแสดงในหน้าจอพอร์ตอนุกรม และตรวจสอบกับผลการวัดบนแบบวาดมาตราส่วน